LUAS SEGITIGA DENGAN TRIGOMETERI ATURAN SINUS DAN ATURAN COSINUS

 Aturan Sinus (Law of Sines atau Sines Law/Rule) adalah teorema berupa persamaan yang menghubungkan nilai sinus sudut dalam segitiga dengan panjang sisi di depannya dalam bentuk perbandingan.

Jika diberikan segitiga sembarang $ABC$seperti gambar, maka berlaku persamaan berikut.
$$\boxed{{\displaystyle {\displaystyle \frac{a}{\sin A}}={\displaystyle \frac{b}{\sin B}}={\displaystyle \frac{c}{\sin C}}=2R}}$$dengan $R$ adalah panjang jari-jari lingkaran luar segitiga $ABC$.

Aturan Cosinus (Law of Cosines atau Cosines Formula/Rule) adalah teorema yang digunakan untuk menentukan panjang sisi depan suatu sudut dengan menggunakan hubungan dua panjang sisi pengapit sudut tersebut dan nilai cosinusnya.

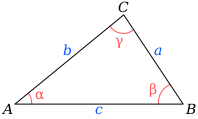
Misalkan $\mathrm{△}ABC$ segitiga sembarang seperti gambar.
Dengan demikian, luas $\mathrm{△}ABC$ dapat dihitung dengan rumus berikut apabila diketahui panjang dua sisi segitiga beserta besar sudut pengapitnya.
$\begin{array}{rl}{L}_{\mathrm{△}ABC}& ={\displaystyle \frac{1}{2}}ab\sin C\\ & ={\displaystyle \frac{1}{2}}bc\sin A\\ & ={\displaystyle \frac{1}{2}}ac\sin B\end{array}$
Luas segitiga juga dapat dihitung bila diketahui panjang satu sisi dan besar tiga sudutnya.
$\begin{array}{rl}{L}_{\mathrm{△}ABC}& ={\displaystyle \frac{a^2\sin B\sin C}{2\sin A}}\\ & ={\displaystyle \frac{b^2\sin A\sin C}{2\sin B}}\\ & ={\displaystyle \frac{c^2\sin A\sin B}{2\sin C}}\end{array}$

Untuk memahami lebih dalam mengenai materi ini, berikut disediakan soal dan pembahasannya. Semoga bermanfaat!

Soal Nomor 1
Diketahui $\mathrm{△}ABC$ dengan panjang sisi $a=4\text{cm}$, $\mathrm{\angle }A={120}^{\circ }$, dan $\mathrm{\angle }B={30}^{\circ }$. Panjang sisi $c=\cdots \cdot$
A. $2\sqrt{2}\text{cm}$                  D. ${\displaystyle \frac{3}{4}}\sqrt{2}\text{cm}$
B. ${\displaystyle \frac{4}{3}}\sqrt{3}\text{cm}$                 E. $\sqrt{3}\text{cm}$
C. ${\displaystyle \frac{3}{4}}\sqrt{3}\text{cm}$

Pembahasan

Soal Nomor 2
Pada $\mathrm{△}JKL$, diketahui $\sin L={\displaystyle \frac{1}{3}}$, $\sin J={\displaystyle \frac{3}{5}}$, dan $JK=5$ cm. Panjang $KL$adalah $\cdots \text{cm}$.
A. $5$                      C. $9$                      E. $15$
B. $7$                      D. $12$

Pembahasan

Soal Nomor 3
Perhatikan gambar $\mathrm{△}ABC$ di bawah ini.
Perbandingan panjang $BC$ dan $AC$ adalah $\cdots \cdot$
A. $3:4$
B. $4:3$
C. $\sqrt{2}:\sqrt{3}$
D. $\sqrt{3}:2\sqrt{2}$
E. $\sqrt{3}:\sqrt{2}$

Pembahasan

Soal Nomor 4
Pada $\mathrm{△}ABC$, diketahui $(b+c):(c+a):(a+b)$ $=4:5:6$. Nilai dari $\sin A:\sin B:\sin C=\cdots \cdot$
A. $7:5:3$                     D. $4:5:6$
B. $3:5:7$                     E. $6:5:4$
C. $7:3:5$

Pembahasan

Soal Nomor 5
Pada $\mathrm{△}ABC$, diketahui bahwa $\mathrm{\angle }B={70}^{\circ }$, $\mathrm{\angle }C={80}^{\circ }$, dan $BC=2$ cm. Jika $R$ adalah panjang jari-jari lingkaran luar segitiga $ABC$, maka nilai $R=\cdots \text{cm}$.
A. $1$                     C. $4$                    E. $10$
B. $2$                     D. $8$

Pembahasan

Soal Nomor 6
Panjang sisi-sisi pada $\mathrm{△}ABC$ berbanding $6:5:4$. Cosinus sudut yang terbesar dari segitiga tersebut adalah $\cdots \cdot$
A. ${\displaystyle \frac{1}{2}}$                     C. ${\displaystyle \frac{3}{4}}$                E. ${\displaystyle \frac{5}{6}}$
B. ${\displaystyle \frac{2}{3}}$                     D. ${\displaystyle \frac{4}{5}}$        

Pembahasan

Soal Nomor 7
Jika panjang sisi-sisi segitiga $ABC$ berturut-turut adalah $AB=4\text{cm}$, $BC=6\text{cm}$, dan $AC=5\text{cm}$, sedangkan $\mathrm{\angle }BAC=\alpha ,$ $\mathrm{\angle }ABC=\beta ,$ dan $\mathrm{\angle }BCA=\gamma ,$ maka $\sin \alpha :\sin \beta :\sin \gamma =\cdots \cdot$
A. $4:5:6$                D. $4:6:5$
B. $5:6:4$                E. $6:4:5$
C. $6:5:4$

Pembahasan

Soal Nomor 8
Dalam sebuah lingkaran yang berjari-jari $8\text{cm}$dibuat segi-$12$ beraturan. Panjang sisi segi-12 beraturan tersebut adalah $\cdots \text{cm}$.
A. $8\sqrt{2-\sqrt{3}}$          
B. $8\sqrt{2-\sqrt{2}}$          
C. $8\sqrt{3-\sqrt{2}}$
D. $8\sqrt{3-\sqrt{3}}$
E. $8\sqrt{3+\sqrt{2}}$

Pembahasan

Soal Nomor 1
Pada suatu segitiga $ABC$, besar $\mathrm{\angle }C$ tiga kali besar $\mathrm{\angle }A$ dan besar $\mathrm{\angle }B$ dua kali besar $\mathrm{\angle }A$. Berapakah perbandingan panjang $AB$ dan $BC$?

Pembahasan

Soal Nomor 2
Diketahui $\mathrm{△}ABC$ dengan $a+c=12$ cm dan $b+c=13$ cm, serta $\mathrm{\angle }A={60}^{\circ }$. Tentukan nilai $a$.

Pembahasan

Soal Nomor 3
Buktikan bahwa dalam segitiga sembarang $ABC$ berlaku ${\displaystyle \frac{a-b}{c}}={\displaystyle \frac{\sin A-\sin B}{\sin C}}$.

Pembahasan

Soal Nomor 4
Buktikan bahwa luas segi empat tali busur $ABCD$ pada gambar di bawah adalah $L={\displaystyle \frac{1}{2}}(ab+cd)\sin \theta$

Pembahasan

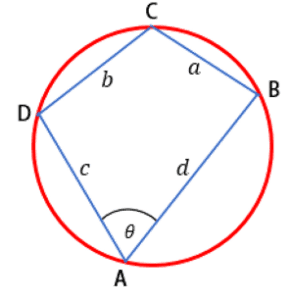
Baca Juga: Soal dan Pembahasan- Persamaan Trigonometri

Soal Nomor 5
Pada gambar di bawah, $ABCD$ adalah segi empat tali busur lingkaran (besar sudut yang berhadapan jumlahnya ${180}^{\circ }$). Buktikan bahwa
$\cos \theta ={\displaystyle \frac{c^2+d^2-a^2-b^2}{2(ab+cd)}}$

Pembahasan

Soal Nomor 6
Diketahui $\mathrm{△}ABC$ dengan $CD$ adalah garis berat, yaitu garis yang membagi dua sama panjang sisi $AB$. Dengan menggunakan Aturan Cosinus, buktikan bahwa:
a. $C{D}^2={\displaystyle \frac{1}{2}}{a}^2+{\displaystyle \frac{1}{2}}{b}^2-{\displaystyle \frac{1}{4}}{c}^2$
b. $4C{D}^2=a^2+b^2+2ab\cos C$

Pembahasan

Soal Nomor 7
Buktikan bahwa luas segi empat $ABCD$sembarang pada gambar di bawah adalah $L={\displaystyle \frac{1}{2}}\cdot AC\cdot BD\cdot \sin \theta .$